퍼셉트론(perceptron) 알고리즘에 관한 내용이다. 퍼셉트론은 프랑크 로젠블라트가 1957년에 고안한 알고리즘이다. 흔히 딥러닝을 시작할 때 퍼셉트론(perceptron)의 개념에 대해서 알고 공부를 한다. 이 고대 화석같은 알고리즘을 왜 배우는가 하면 이는 퍼셉트론이 신경망(딥러닝)의 기원이기 때문이다.
1. 퍼셉트론이란?
퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력한다. 이 책에서는 흔히 신호를 전류나 강물처럼 흐름이 있는 것으로 상상하는게 좋다고 하나, 본인은 그런 상상은 잘 안든다..
우선 퍼셉트론은 입력이 0과 1로 두가지 값을 갖을 수 있다.
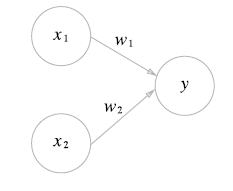
위 그림에서
-x1 과 x2는 입력 신호, y는 출력 신호, w1과 w2는 가중치를 의미한다.
-원을 뉴런 또는 노드라고 부른다.
-입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다.(x1*w1,x2*w2).
-뉴런에서 전달 받은 신호의 총합이 임계값 theta를 넘을 때만 1을 출력한다.
이를 수식으로 나타내면,
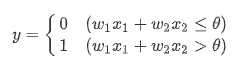
퍼셉트론은 복수의 입력 신호 각각에 고유한 가중치를 부여한다. 가중치는 각 신호가 결과에 주는 영향력을 조절하는 요소로 작용하며, 가중치가 클수록 신호가 그만큼 더 중요함을 뜻한다.
2. 단순한 논리 회로
AND 게이트
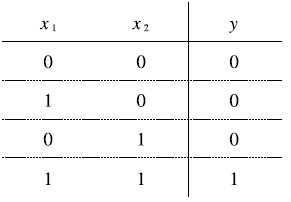
이 그림은 AND게이트의 진리표로, 두 입력이 모두 1일 때만 1을 출력하고 그 외에는 0을 출력한다.
NAND 게이트와 OR 게이트
NAND 게이트는 Not AND를 의미하며, 그 동작은 AND게이트의 출력을 뒤집은 것이다.
진리표로 확인해보면,

위 그림처럼 x1과 x2가 모두 1일 때만 0을 출력, 그 외에는 모두 1을 출력한다.
OR 게이트는 입력 신호 중 하나 이상이 1이면 출력이 1이 되는 논리 회로이다.
진리표를 확인해보면,

3. 퍼셉트론 구현하기
3.1 간단한 구현.
위에서 배운 논리 회로를 간단하게 파이썬으로 구현해보자.
def AND_Func(x1,x2):
w1,w2,theta=.5,.5,.7
tmp=x1*w1+x2*w2
if tmp<=theta:
return 0
elif tmp>theta:
return 1위 함수는 x1과 x2를 인수로 받는 AND_Func함수이다. 매개변수 w1,w2,theta는 함수 안에서 초기화하고, 가중치를 곱한 입력의 총합이 임계값을 넘으면 1을 반환하고 그 외에는 0을 반환한다.
inputs=[(0,0),(1,0),(0,1),(1,1)]
for x1,x2 in inputs:
y=AND_Func(x1,x2)
print('({x1},{x2})->{y}'.format(x1=x1,x2=x2,y=y))
(0,0)->0
(1,0)->0
(0,1)->0
(1,1)->1다음 과 같이 input튜플리스트를 만든 후, 이 값을 차례로 AND_Func에 집어넣으면 위와 같은 출력값이 나온다.
3.2 가중치와 편향 도입
앞에서 구현한 AND게이트는 직관적이고 알기 쉽지만, 다른 방식으로 수정해보자.
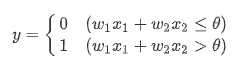
위 식에서 theta를 -b로 치환하면 퍼셉트론의 동작은 다음과 같다.

기호 표기만 변경되었지, 그 의미는 같다. 여기서는 b를 편향이라고 하며 w1과 w2는 그대로 가중치이다.
해석해보면, 퍼셉트론은 입력 신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력, 그렇지 않으면 0
을 출력한다. 파이썬으로 확인해보자.
가중치와 편향을 도입한 AND gate
import numpy as np
def AND_Func_Bias(x1,x2):
x=np.array([x1,x2])
w=np.array([.5,.5])
b=-.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1위 함수는 theta가 -b로 치환된 함수이다. 또한, 편향은 가중치와 다르다는 사실에 주의하자. 구체적으로 설명하자면 w1과 w2는 각 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수고, 편향은 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조절하는 매개변수이다. 추가적으로 과녁의 예를 들 수있다. 이는 통계학 카테고리에 따로 설명을 해놓겠다.
inputs=[(0,0),(1,0),(0,1),(1,1)]
for x1,x2 in inputs:
y=AND_Func_Bias(x1,x2)
print('({x1},{x2}=>{y})'.format(x1=x1,x2=x2,y=y))
(0,0=>0)
(1,0=>0)
(0,1=>0)
(1,1=>1)
가중치와 편향을 도입한 NAND gate & OR gate
def NAND_Bias_Func(x1,x2):
x=np.array([x1,x2])
w=np.array([-.5,-.5])
b=.7
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
def OR_Bias_Func(x1,x2):
x=np.array([x1,x2])
w=np.array([.5,.5])
b=-.2
tmp=np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
#NAND
for x1,x2 in inputs:
y=NAND_Bias_Func(x1,x2)
print('({x1},{x2}=>{y})'.format(x1=x1,x2=x2,y=y))
(0,0=>1)
(1,0=>1)
(0,1=>1)
(1,1=>0)
#OR
for x1,x2 in inputs:
y=OR_Bias_Func(x1,x2)
print('({x1},{x2}=>{y})'.format(x1=x1,x2=x2,y=y))
(0,0=>0)
(1,0=>1)
(0,1=>1)
(1,1=>1)
4. 퍼셉트론의 한계
XOR 게이트
XOR 게이트는 배타적 논리합이라는 논리 회로이다. x1과 x2 중 한쪽이 1일 때만 1을 출력한다. 즉 자기 외에는 거부한다는 의미이다.

이 XOR게이트로 우리는 퍼셉트론을 구현하려면 가중치 매개변수 값을 어떻게 설정할까? 사실 지금까지 본 퍼셉트론으로는 이 XOR게이트를 구현할 수 없다.
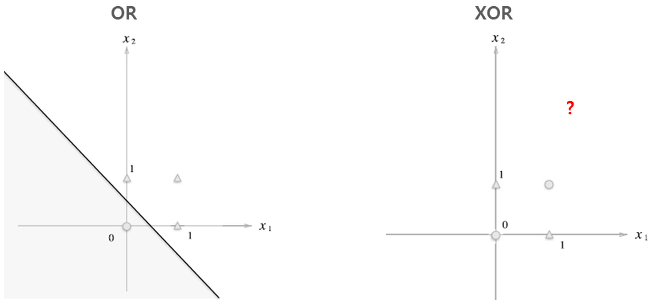
즉, 단층 퍼셉트론으로 AND,NAND,OR 게이트는 구현 가능하지만, XOR게이트는 구현할 수 없다. 퍼셉트론은 위와 같이 직선으로 나뉜 두 영역을 만든다. 하지만 XOR은 직선으로 두 영역을 나눌 수 없다.
선형과 비선형

퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다는 한계가 있다. 위 그림과 같은 곡선은 표현할 수 없다는 의미이다. 위 그림과 같은 곡선의 영역을 비선형 영역, 직선의 영역을 선형 영역이라고 한다. 선형, 비선형이라는 말은 기계학습 분야에서 자주 쓰이는 용어이다.
다층 퍼셉트론
퍼셉트론의 아름다움은 '층을 쌓아' 다층 퍼셉트론을 만들 수 있다는데 있다. 우선, XOR 게이트 문제를 다른관점에서 생각해보자.
-기존 게이트 조합하기
XOR 게이트를 만든느 방법은 다양하다. 그중 하나는 앞서 만든 AND,NAND,OR 게이트를 조합하는 방법이다.
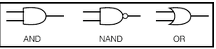

위 조합이 정말 XOR를 구현하는지 살펴보자. NAND의 출력을 s1, OR의 출력을 s2로 해서 진리표를 만들면 밑에 그림처럼 된다.
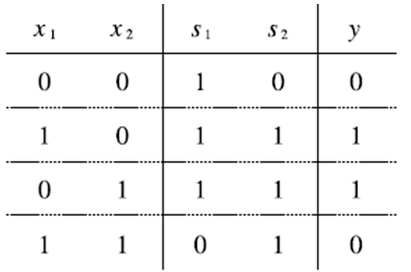
-XOR 게이트 구현하기
def XOR(x1,x2):
s1=NAND_Bias_Func(x1,x2)
s2=OR_Bias_Func(x1,x2)
y=AND_Func_Bias(s1,s2)
return yfor x1,x2 in inputs:
y=XOR(x1,x2)
print('({x1},{x2}=>{y})'.format(x1=x1,x2=x2,y=y))
(0,0=>0)
(1,0=>1)
(0,1=>1)
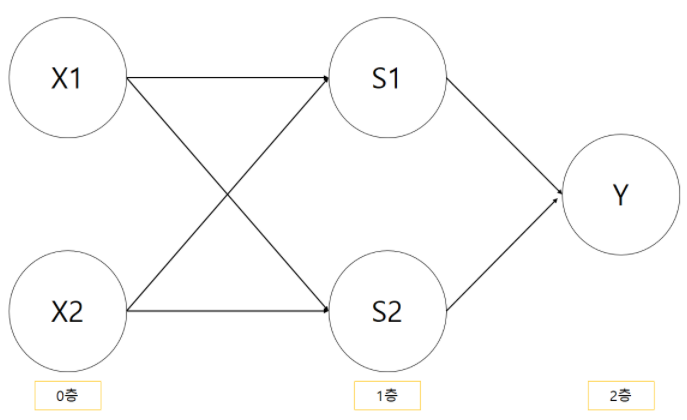
(1,1=>0)이로써 XOR 게이트를 완성했다. 지금 구현한 XOR를 뉴런을 이용한 퍼셉트론으로 표현하면 다음과 같다.
'Deep Learning > 밑바닥부터 시작하는 딥러닝(1)' 카테고리의 다른 글
| Chapter 6. 학습 관련 기술들(1) (0) | 2021.03.02 |
|---|---|
| Chapter 5. 오차역전파법 (0) | 2021.01.25 |
| Chapter 4. 신경망 학습 (0) | 2021.01.23 |
| Chapter 3-2 다차원 배열의 계산 (0) | 2021.01.18 |
| Chapter 3-1 신경망 (0) | 2021.01.17 |